Music by numbers

On this page

Some books tying music and mathematics together (reviews in the order I wrote them)

Robert Osserman - "Poetry of the Universe"
Jamie James - "The Music of the Spheres"
Thomas Levenson - "Measure for Measure"

I was partly spurred into thinking about this by some nonsense I found about crop circles and "diatonic ratios". Claims that "no-one had ever previously linked mathematics to music" and stuff like that. Jamie James' book is the best to read as an antidote. Osserman is a close second, and Levenson a near miss.

"Only gather 2, 3, 4, and 5 together, and the mumbo-jumbo artists of the world will construct a theory, a conspiracy, or a piece of magick."

Making scales - Honest, yet ill-fitting work on the numbers
Semitone calculator - Converts frequency (and harmonic) ratios to semitones
The pentatonic scale - How is it really built?
Crop circles - "Diatonic ratios" perhaps, but fairly obviously bogus

Robert Osserman

"Euler and Bach lived in the eighteenth century and, as was traditional at the time, they worked under the patronage of the nobility or royalty."
"Beethoven and Gauss, by contrast, personified the romantic ideals of the early nineteenth century."
"Brahms and Riemann are much more solidly situated in the mid- to late-nineteenth century world. Peering at us over their full beards..."

Thus begin the 2nd, 3rd, and 4th paragraphs of Chapter V, "Curved Space", of Robert Osserman's "Poetry of the Universe: a mathematical exploration of the cosmos." Surely no ordinary book could juxtapose these six Germanic heros? If you don't see how the universe could expand from a "big bang" without having edges, this is the book for you, but even if you think you do (see), it's a wonderful little read. He starts off with some interesting bits about map projections [private joke deleted: see more about projections], and takes us on a cosmological journey through fractals, non-Euclidean geometry, and computer games played on a torus.

For those who might think this sort of thing is a guide, none of Dawkins, Dennett, Hofstadter and Gould appears in the index, but MC Escher, Albert Einstein, Richard Feynmann, Harry Kroto (of buckeyballs fame), Adolf Hitler, Pope John Paul II, Pac-man, William Wordsworth, and Zu Chongzhi* are among the many luminaries who do. Highly recommended.

* Chinese characters appear on the right. (His name is Tsu Ch'ung-Chi in Wade-Giles romanisation, read So Chuushi in Japanese.) Lived AD 430 to 501, and obtained the approximations 22/7 and 355/133 for pi.

(Posted to the PandA mailing list, 11 Mar 1998)

In my bookshelf - Amazon.com (USA) - Amazon.co.uk (UK) - Amazon Japan (Popup help)

Jamie James

Book cover "The Music of the Spheres" covers an immense sweep of history, from Pythagoras to Karlheinz Stockhausen. While Osserman in the preceding book gives us a musically enlightened view of mathematical physics, here James gives us a mathematically enlightened view of music.

The relation of number to music runs all through this book, starting with the story of how Pythagoras was passing a blacksmith's, and noticed that the note given out by a piece of iron on the anvil was determined by the weight of the hammer hitting it. Thus a hammer of twice the weight produces a note an octave higher. James keeps us suspended for sixty pages and 2000 years before revealing that Vincenzo Galilei (Galileo's Dad) pointed out that this is all wrong (but then went on to make some mistakes of his own).

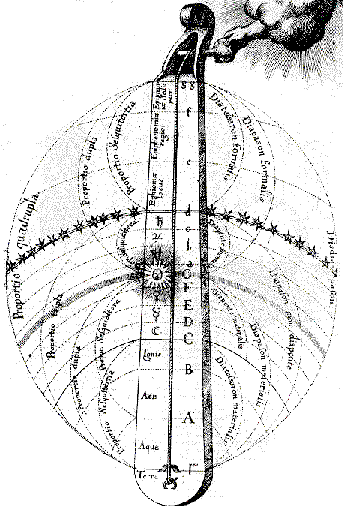The Divine Monochord, by Robert Fludd

Such factual infelicities weren't allowed to get in the way much in ancient Greece, it seems. It's hard to assess some aspects of this, since we have no reliable records of what the performed music of the time sounded like. (Imagine discussing Greek sculpture with only diarists' descriptions to go on!) Pythagoras and (or?) his secretive band of followers were concerned not with the vulgar stuff of musica instrumentalis, but with musica mundana, the music of the spheres, the ethereal, inaudible ground of the universe. The assumption that numerology explains everything runs all the way through to Chapter 8, "Kepler Pythagorizes". To today's blinkered empiricist, one piece of numerology resembles another, simply because there is only one set of integers, but the universal working assumption in the time of Kepler (1571-1630) was that God left his telephone number (as it were) in the workings of the heavens.

Kepler discovered, as he thought, the secret of the arrangement of the planets. There are (were) six - Mercury, Venus, Earth, Mars, Jupiter, and Saturn - and there are five platonic solids - tetrahedron, cube, octohedron, dodecahedron, and icosahedron - so obviously the polyhedra must fit between the spheres including the circles around which the planets move. At this point the assumption would appear to be that the musical intervals corresponding to the ratios of the diameters of the spheres were those that produced the "cosmic harmony". But when the same Kepler discovered that the planets orbit in ellipses and not in circles, rather than abandoning the idea, he simply generated more "musical intervals". For example, the ratios of the minimum and maximum angles that a planet revolves about the sun in a period of 24 hours (i.e. the relative angular speeds at aphelion and perihelion) gave him more ratios. It didn't seem to matter whether they gave a harmonious interval (Saturn: major third) or just a number something to do with music (Venus: the Pythagorean comma). Meanwhile, his contemporary Robert Fludd, creator of the Divine Monochord (above), played even looser with his sums. Rather as I've compared James and Osserman above, here James talks of Kepler's "magic-tinged mathematics" versus Fludd's "vaguely mathematical species of magic."

After a chapter on Newton and The Magic Flute (Masonic connections), James takes us on to another major theme of his book: "The Romantic Anomaly". To make a gross summary: before Beethoven, the job of music was to present a human-hearable approximation to the divine reality of music, which could of course be immediately appreciated by anyone. From Beethoven on, the direct portrayal of this absolute beauty was replaced by a more human-centred portrayal of the artist's personal and human struggle to understand this beauty. A bit like the difference between mathematics and literary criticism, and as he convincingly points out, accompanied by some of the same pseudo-intellectual claptrap that hovers around lit. crit. - it was only with the Romantic era that the musical snob was born. As a historical description of changes in thinking, this is an extremely interesting chapter, but I can't say I feel the "anomaly" claim is proved. The argument goes, that when Schoenberg (in particular) rejected tonality, this was the beginning of the return to "pure" music.

I think the story of Schoenberg is quite well known. After writing some of the latest and greatest music of the Romantic era - Gurrelieder (with which I'm not familiar, or Verklaerte Nacht with which I am) - Schoenberg asserted: "Tonality does not serve; it must be served." So in its place he invented a completely new system of music. The blinkered empiricist's eyebrows rise, of course, when it turns out this largely means a return to numerological nonsense. But whereas numerology from Pythagoras to Kepler was a post hoc affair, fitting numbers to music that already existed, Schoenberg confidently assigned predictive force to the numerology, and used it to generate something.

Why twelve-tone composition? According to Schoenberg, one "magic" fact about twelve is that the "digits" add up to three. Oh, yes? So the magic on which the universe is based has a particular penchant for expressing numbers in decimal notation, does it? In reality the twelve semitones that make up the equitempered scale on a piano keyboard simply represent an engineering kludge: if you want a mathematical key, it is the untidy fact that 1.5¹² is roughly equal to 2⁷. (That is, twelve fifth intervals roughly equal seven octaves. The ratio indicating the discrepancy between these numbers is the Pythagorean comma.) But does this music "work"? Must it work? Could it work?

There does seem to be a logical error in assuming that it must work; there is a simple mathematical model behind tonal/harmonic music, but it does not follow that given a mathematical model plucked from the air a sort of music will necessarily emerge in front of it. David Littleboy pointed out an interesting analogy with natural language, here. The mathematical basis to harmony, and indeed to the temporal structure of traditional music is recursive in nature. That is, to remember "where you are" only requires a limited stack of bits yet to be resolved. This means that more complicated patterns are made by nesting one structure within another, just the way that natural language works. But the rule of twelve-tone music, that every one of the twelve must appear exactly once, can only be apprehended by counting. Chomsky puts much weight on the fact that natural language doesn't operate with rules that require counting, such as "To make a sentence negative, insert 'not' as the fifth word." Rather the rules require a nested, recursively defined structure. According to Chomsky, and his followers, this is a biological fact, and shows that language is provided by a special human "language module" in the brain. It's interesting, then, that the music we arrived at by discovery is distinguished in just the same sort of way from twelve-tone music, which was arrived at by invention.

But could it work? I have a suspicion that the human learning mechanism is vastly more flexible than Chomsky's view (in particular) allows. Here's a little experiment I did quite a few years ago now. I was writing some software (in the days of MS-DOS, no multitasking user interface), and for test purposes I needed to monitor the progress of a sorting operation going on in the background. So I wrote a little 'beep' routine, that indicated each step by a rise in tone. Instead of multiplying the frequency by say 12th-root of 2 for a semitone, I used the fifth root of two. This makes a truly weird, even-spaced, scale, which of course cannot be played on the piano or written in conventional notation. But I heard it (passively) many times. By the time the program was up together, of course, I was so used to this progression it was beginning to sound musical. My suspicion is that however arbitrarily you constructed a system, given the appropriate luck it could attract followers.

Anyway, an excellent read!

In my bookshelf - Amazon.com (USA) - Amazon.co.uk (UK) - Amazon Japan (Popup help)
This is also in my "Top Ten" list of books everyone should read to understand the world we live in.

Related non-music books

Noam Chomsky, "Language and problems of knowledge", pub. MIT, 1988. Eminently readable - Chapter 2 discusses the kind of distinction mentioned above.
Steven Pinker, "The Language Instinct"

Thomas Levenson

Book cover I read Thomas Levenson's "Measure for Measure - a musical history of science" some while ago. It's very much in a similar mould to the two books above, but despite some interesting bits just doesn't match up. As the subtitle suggests, though, it is more about science with musical connections than music with scientific connections

After going through the standard bit about Pythagorus walking past the blacksmith's, he describes Leonard Bernstein's theory of the origin of the pentatonic scale. Unfortunately, this involves a number of flaky claims, which we'll look at below, and is shortly followed by a description of a Greek invention - the organon - for providing a better compressed air supply. Frankly I didn't try very hard to understand this: with no diagram, and an indefinite number of chambers and things, it didn't seem worth bothering with. (Reminds me, though, that some time I must investigate the mysterious chamber on the side of a typical Japanese bicycle pump.) Then we get to page 101 and find this startling statement:

"The human eye has a focal length of about 10 inches or 250 millimeters..."

Apparently Levenson thinks "focal length" means "a length, uh yes, a distance, uh yes, measured, uh somewhere, anywhere, near a lens." (There's an explanation of focal length in the Truth on my "Close-up filter" page.)

Levenson is discussing the microscopes created by Antoni van Leeuwenhoek (He writes "Antony", but a Google search in Dutch shows Antoni to be far the commonest form), and he asserts that the magnification of one of Leeuwenhoek's microscopes (actually a simple lens) is determined by the ratio of the "focal length" (by which he obviously means minimum viewing distance) of the eye by the focal length of the microscope lens. Perhaps he means well, but just has the terminology wrong.

We can check this, with my Popup lens calculator (More details: "Close-up filter" page)

From the optical centre of the lens to the centre of the retina in the human eye is about 17 mm (according to another book I have here), meaning the focal length is 17 mm when focussed at infinity. First, in the upper calculator set the object distance to 250 mm and image distance to 17 mm, and note the magnification: x0.07. Now find the focal length of the combination of the eye lens (17 mm: after cheating by looking at the answer, we suppose that with Leeuwenhoek's microscope one focusses at infinity) and microscope (25 mm) in the lower calculator: 10 mm. Now plug this back into the upper calculator, keeping the image distance at 17 mm: lo and behold, magnification is x0.7. This figure, of course is the relative size of the image on your retina, and it is just ten times the naked eye figure.

Anyway, Levenson's book is like that - many interesting things in it, but you need to check his working.

In my bookshelf - Amazon.com (USA) - Amazon.co.uk (UK) - Amazon Japan (Popup help)

This painting by Vermeer (at bottom of page) may be of Leeuwenhoek.

The Numbers - making a scale

8 - 2 = 5 ?

Here are some curious dictionary entries: the first two are from the Longman Dictionary of the English Language, but you will find similar versions in other dictionaries.
Diatonic "...scale of eight notes to the octave..."
Pentatonic "...musical scale consisting of five tones..."
Yonanuki "four-and-seven-missing" - a Japanese term for "pentatonic" (see my jeKai entry)
So removing the fourth and seventh notes (2, ok?) from the diatonic scale (8, right?) makes the pentatonic (5, isn't it?), hence the equation at the top...

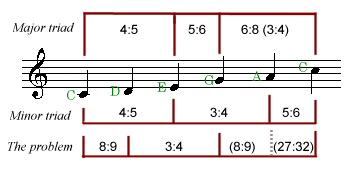
This apparent anomaly is due to the fact that in general musical terminology uses inclusive counting for intervals. This makes the arithmetic at odds with naive expectations ("a third plus a third is a fifth"), but it's perfectly internally consistent, which makes it mathematically OK.

The problem with the numbers is not that they are too complicated - rather they are too simple. This makes it just too easy to create plausible-looking claims with no real basis in fact (or mathematics). This section is about attempts at mathematical explanation which may not quite work, yet appear to be honest; if you want to see the other possibility, skip down to the bit on crop circles.

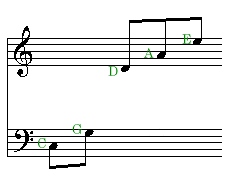
Let's take a couple of fairly typical attempts to explain where the pentatonic scale comes from. The scale we are looking for is equivalent to the black notes on the piano, starting from F#, but for convenience we'll do this in the key of C, with the white-note sequence C-D-E-G-A.

Leonard Bernstein via Thomas Levenson (It's not clear how accurate the reporting is.)

The first six in the series of overtones, the octave, the fifth, the fourth, the third, and the next one, the second, create a five-note "pentatonic" scale.

Well, it's not clear how the octave helps, since it just gets us to the "same" note. But notice the seductively neat progression: "fifth, fourth, third, and the next one..." Trouble is, what does this mean?

The first eight harmonics

Look at the diagram on the left, where I've shown the first eight harmonics (on rather, their closest equivalents on the piano keyboard), with the intervals between them. The octave takes us from C to C, then the interval of a perfect fifth from harmonic 2 to harmonic 3 goes from C to G. Good, so after three harmonics, two overtones, and two intervals, we have two notes.* Then the next interval is a fourth, just like he says, but it takes us back to C again! And the next - indeed a major third - takes us to E (3 down, 2 to go), then a minor third, back to G. Finally, the interval from the fifth to sixth overtones (labelled harmonics 6 and 7) gets us to approximately B flat; no relation to reality, even if we put aside the mystery of how the interval from harmonic 6 to 7 got to be called a second. (As you can check with the calculator below a frequency ratio of 7/6 is approximately 2.7 semitones, closest to a minor third.)

* Perhaps with a bit of work, I could write this stuff with the numbers in bold, then at the end say "Hey! See how I've written the first twenty digits of pi."

Next, Steven Pinker in "How the Mind Works" If Levenson can defend himself by claiming to have forgotten Bernstein's exact words, Pinker has an explicit disclaimer - "At least, this is a popular explanation of where musical scales come from; not everyone agrees." he says at the end.

f₀ : fundamental - harmonic 1

f₁ : 1st overtone - harmonic 2

f₂ : 2nd overtone - harmonic 3

Harmonics in a vibrating string

Plenty of numerical oddities, anyway. First let's clear up a standard confusion: harmonics and overtones. In physics, the different modes in which a string (say) can vibrate are called the harmonics, and numbered from 1, being the fundamental, then the second harmonic has twice the frequency, and so on. In music, it is more usual to talk of overtones, and on the violin for example, to get the first overtone, you put your finger very close to the mid-point of the string: this forces it to vibrate as shown in the second shape shown in the figure on the right. Unfortunately, this technique of putting a finger on the string gets called "harmonics" as well, and so there is a conflicting terminology in which the first overtone is called "first harmonic". (Just something to watch for, but I remember coming badly unstuck translating something involving harmonics when I was used to the musical terminology.)

Pinker then: on page 530 in my Penguin paperback he is explaining harmonics, and says - "Say the fundamental frequency is 64 vibrations a second, the second C below middle C on the piano." He then refers to the overtones, using the number in the figure above. But on page 531 he says: "The seventh overtone of our reference note (448 vibrations a second) is close to middle A (but, for complicated reasons, not exactly at it)." I count four mistakes so far.

He's fallen in the "overtone/harmonic" trap - he means seventh harmonic.
Unfortunately, his figure of 64 Hz for C is only a rough approximation: actually it's about 65.4, because standard concert pitch is based on A being 440 Hz. (Check by entering these two values in the calculator below, getting an almost exact number of semitones.)
If you simply enter 7 and 1 for the frequencies in the calculator, you get the interval for the seventh harmonic: "2 octaves + minor 7th". So far from being not exactly the A, at 9.688 semitones over the two octaves, it's closer to B flat. (Actually 7 x 65.4 = 457.8, even further from A=440 than 448.)
It seems inaccurate to claim "complicated reasons". If you agree that the pentatonic scale is built as below, it's simply that the natural A in the pentatonic is a major third (5/4) with a perfect fourth (4/3) on top of it, making 5*4/(4*3) = 5/3 ratio, whereas the seventh harmonic is 7/4. That's a discrepancy of 21/20: almost a semitone. (Check it!)

His next claim isn't very plausible, either: that the diatonic scale is made by "filling in the gaps" in the pentatonic scale with the next "distinct harmonics" being F and B. It is vastly more likely that F arrives as a natural perfect fourth, that is, a 4/3 ratio above C. And the situation for B is already muddled, because the 7th harmonic is a bad fit for B flat, so to get a not terribly good fit for B natural we have to wait for the 15th harmonic, skipping a whole pile of potentially useful harmonics in between. This is really dreadfully unconvincing.

Well, that's enough complaining. Here's the calculator, then I'd better try to come up with a better story myself.

Steven Pinker's books: In my bookshelf

Semitone calculator

The pentatonic scale

C-G-D-A-E
Pentatonic - the tower of fifths

How is it really built? Well, there are a number of ways it could be built, and I rather guess that historically things haven't always been as clear as they might be. But anyway, rejecting the version Pinker gives above as utterly implausible, at the opposite end of the spectrum (as it were), the very simplest way to get the set of notes in the C-D-E-G-A-C pentatonic is with a tower of fifths as on the left. (These are the notes of the strings of a cello and violin - in different octaves - which is why this sounds a bit like the orchestra tuning up.) Some versions of the pentatonic surely do use this "tower of fifths"; in particular if you are using the middle note of the tower (D in the case of C-G-D-A-E) as the base note. But when the bottom of the tower (C here) is the base, because the step between each pair of these notes is a 2:3 frequency ratio, the top of the tower (E) is in a 64:81 relation to C. Tantalizingly close to 4:5 (or 64:80).

C-D-E-G-A-C

Well, that's it, really: if only this were a pure fifth harmonic, the C-E-G would make a perfect major triad, as shown in the figure on the right. Take a look at the numbers in these ratios: 4:5 - 5:6 - 3:4. What makes this special (both mathematically and musically) is that the ratios are numerically simple, meaning close harmonic relations, but when you multiply the fractions together, everything cancels out except a single 2 (for the octave). This makes me want to fit the A in the same way, to make the minor triad C-E-A shown under the stave. That gives us the best harmonic possibilities, but how does the D fit in? The problem comes in trying to fit the A in with the D: as shown in the bottom row in the figure, since the only possible harmonic relationship of D to A is 2:3, this leaves A at 16:27, and the interval to get back to C is 27:32 in its simplest terms. So there is no simple harmonic relationship. Actually, the best triad is simply C-D-G-C, with the ratios: 8:9 - 3:4 - 3:4. To ears accustomed to "Western" music, this is a discord, but sure enough, it's a basic element of some Japanese music (which I am just getting used to in rehearsals).

Confession: I simply don't know which of the two above versions is more true to historical practice, but I have failed to find any definitive description, so this is my own exploration. I have tried to take a bit more care than seems to be usual with arithmetic claims, but if I am wrong anywhere, I hope someone will point it out. To sum up: I can see two ways of selecting the E in the above example, with the 80:81 comma between them. For the A, I think either the tower of fifths version (16:27) or the harmonic version (3:5) is plausible, with the same 80:81 comma. The 7th harmonic story (4:7) seems extremely unlikely, since it is more than half a semitone away.

The Numbers - ah, crop circles

In a mailing list discussion way back in March 1998, someone referred to the following web page, and said: "Here's one that needs the scrutiny of a knowledgeable mathematician." Here's my response, only edited to add some links.

Here's a link: Gerald Hawkins' work on crop circles and their relationship to Euclidean geometry and diatonic ratios (You will need to get the page, to look at the diagrams.)

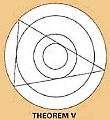
Theorem V
(V) As the triangle changes shape the circles expand and contract to touch the sides, and the diagram generates the four crop circle theorems.

Sample: Diagram and caption from Hawkins' page

On the left of Hawkins' page is a set of five diagrams, labelled "Theorem I" to "Theorem V". Only theorem V seems to have any text associated with it, and this is an explanation of the way in which the diagram is generic, rather than a text which looks like a conventional theorem. This is the first problem: these do not appear to be "theorems" at all in the accepted sense. For example, Theorem II has an outer circle, inside which is inscribed an equilateral triangle (i.e. its corners touch the outer circle), inside which is inscribed an inner circle. That's it. Huh? Where's the theorem?

A theorem is a "general result": a geometric theorem can be quite simple, and shown by a single diagram, but it needs a description of just what the general result is. A highly recommended book full of examples is the Penguin Dictionary of Curious and Interesting Geometry, by David Wells (a friend of mine, not that that's relevant). The theorem I proved the other day with the bubbles and menu on a dinner table is a good example.

Anyway, never mind, let's try to press on. Back to the text.

I can't resist pointing out that the first sentence contains a very obvious typo: "This document contains a substantial amount outstanding photographic evidence." Plainly this proves nothing about anything, though it is symptomatic of a general inability to spell (and I don't just mean "it[']s" - we are introduced to an Italian mathematician called Fabionacci [sic]), which in turn suggests a general lack of care.

Anyway, the meat of this page...

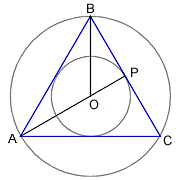
Several years ago, astronomer Gerald S. Hawkins, former Chairman of the astronomy department at Boston University, noticed that some of the most visually striking of the crop-circle patterns embodied geometric theorems that express specific numerical relationships among the areas of various circles, triangles, and other shapes making up the patterns (Science News: 2/1/92, p. 76). In one case, for example, an equilateral triangle fitted snugly between an outer and an inner circle. It turns out that the area of the outer circle is precisely four times that of the inner circle.

Equilateral triangle two circles
ABC is an equilateral triangle, P is the mid-point of one side, so AB = 2 PB; angle BPO is 90 degrees. Triangles APB and BPO are similar (angles are the same), so BO = 2 PO. QED.
Incidentally, by drawing the circles first, this diagram was extremely simple to generate, contrary to the flim-flam on the left.

Sketch of proof that radii are in ratio 1:2

Never mind whether the term "theorem" is appropriate, the result here seems to be that the area ratio is precisely 4:1. Or more simply, the radii are in the ratio 2:1. Indeed. To put it another way, if you make two circles, one inside the other and of half the radius, then an equilateral triangle fits between them. (Of course it does: from the centre of an equilateral triangle to a vertex is twice the distance to the mid-point of a side, as the figure on the right shows.) It's unclear to me whether a crop circle has appeared with the pattern of this "Theorem" including the triangle, or simply one in which two circles had radii in the ratio 1:2.

Three other patterns also displayed exact numerical relationships, all of them involving a diatonic ratio, the simple whole-number ratios that determine a scale of musical notes. "These designs demonstrate the remarkable mathematical ability of their creators," Hawkins comments.

Theorem I is a bit mysterious - it looks to me as though the figure is wrong; Theorems III and IV have two concentric circles with a square and a regular hexagon fitting between them. It's trivial in these cases to work out the ratio of the radii: root(2):1 and 2:root(3). But Mr Hawkins prefers to square these values, getting 2:1 and 4:3. Fine, though one has to ask why he squares them? (Presumably it couldn't simply be because that gives him what he wants?) And it's not clear to me quite what the "remarkable mathematical ability" is? Is it the ability to construct shapes with ruler and compasses?

Hawkins found that he could use the principles of Euclidean geometry to prove four theorems derived from the relationships among the areas depicted in these patterns. ...

The web page claims that the "fifth theorem" has been published by the American National Council of Teachers of Mathematics: I sent an email request for the written proof, but this turned into a wild goose chase. I've tried asking again.

What is most surprising is that all geometries give diatonic (musical) ratios. Never before have geometric theorems been linked with music.

The claim that XYZ has "never been thought of" is easy to make. One would not think though that people would make claims quite so easy to refute. On the shelf behind me is another highly recommended book: "The music of the spheres", by Jamie James, which tells us that geometric [not-quite-theorems, are they] have been being linked with music since, um, gosh, about 2500 years ago.

On this page there are a couple of "glossary" links, one for "geometric theorems". This is headed "Definitions", and the first definition reads as follows:

A Crop geometry is an unembellished diagram with rotational symmetry, which contains a theorem that can be proved by Euclidean logic and constructions, and generally leads to a pair or more of diatonic ratios.

This strikes me as, at the very least, very sloppily written. Does it mean that the diagram includes a construction which can be used to prove some result -- of some generality? of no generality at all? He doesn't define "embellished". The other definitions are equally obscure. This is not mathematical writing.

My opinion is (and this is actually unrelated to the wider issue of crop circles) that this page is close to vacuous. So what do I make of the bits I can't make much of? Perhaps all the stuff about bending stalks is where the Truth lies hidden? Should I go on to analyse the page this leads to about "The relationship between diatonic ratios, crop circles and the Society for Psychic Research"??

(Posted to the PandA mailing list, 24 Mar 1998)

Want to know more?

This interview with Gerald Hawkins on a New Age website is quite funny.

The Moral

There isn't a moral, except not to believe everything you read on the Internet. I'm aware that this is rather unfinished - there's been time since I wrote the first bits to change my mind entirely. I'm currently getting some "hands on" experience of the pentatonic in rehearsals for our local musical Ennin to be performed in January 2002, so I hope to follow up with some more concrete ideas.

Meanwhile: Get a portrait of Gauss!