What is a close-up filter?

Bowl
Coming soon: "How to alter perspective with a wide-angle lens"

I remember (many years ago now) just wanting to photograph a map using an old 35-mm camera (not an SLR), with a close-up lens attachment on the front. It was a terrible fiddle, with all sorts of troublesome calculations (see Boring Grey Box below) to get the focus right. Surely modern technology can produce something much easier to use? Yes, it can and it has! It's called a "close-up filter", and it takes advantage of our new understanding of stuff like quantum mechatronics.

So how does it work? How can a mere filter affect things like focal lengths?

I'm glad you asked that question. As you know, light consists of photons, which bounce around just like billiard balls, and just like billiard balls, as photons travel they lose energy. In fact, this is what we call the "inverse square law" of light fall-off. (Nobody quite remembers how it got that name, but it's probably to do with an obsolete camera that used a mirror instead of a lens, and took square pictures. Oh, and the image was upside-down in the viewfinder.) It means that each time the photon doubles the distance it has travelled, it loses a measurable quantum of energy. And the new "close-up filters" are sensitive to these quantum levels, and only let through photons fully-charged with energy. That's why they let you take sharp photographs of flowers and insects, while the lower-powered photons from the background turn into a kind of fuzz, or bokeh* as it's technically known. The best of it is, of course, that you can skip all the old-fashioned grey stuff below about "focal lengths" and concentrate on being creative.

* Linguistic note: The original Japanese term boke (the 'h' is superfluous, as long as you don't pronounce it to rhyme with "broke") also refers to what happens to people who have become grey and boring, and lost their normal mental faculties. Sort of like the photons.

Another linguistic note: How is it pronounced, then? "Boke(h)"? Well, in British English pronunciation, imagine the words "botch" and "ketch", then string them together with the "-tch" bits omitted. (If you're an American speaker the first part is probably closer to "boat" with the t missing.)

Boring Grey Box

The old-fashioned way

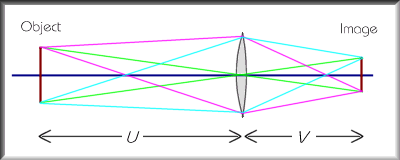1/u + 1/v is constant The picture on the right shows roughly what happens when some object (it should really be a tulip, but I can't draw, so you'll have to do with the maroon line) forms an inverted image on the opposite side of a converging lens. The green lines show how rays pass straight through the centre of the lens (exactly as though it were a pinhole); the purple lines show rays from the top of the object being squashed back to focus on the bottom of the image, and similarly the cyan lines from bottom to top. The idea, if the object is something interesting, is to put the film in your camera just where the in-focus image will appear on it.

In days of yore, blinkered empiricists investigated the relation between the distances u and v to the object and image from any particular lens, and discovered that 1/u + 1/v stayed constant, as the distances varied. In particular, if the object is "at infinity" - in other words when the light rays from any part of it are parallel, as accurately as can be measured, then the distance to the image is called the "focal length", and given the symbol f. If u is infinity and v = f, then since 1/u is zero, we get the basic rule, which is all we have to memorise:

1/u + 1/v = 1/f

From this one equation, we can immediately answer about half the questions in photography groups about extension tubes and suchlike. Suppose we have a camera with a 50 mm lens (f = 50 - we'll work in millimetres), and we stick a 36 mm extension tube between the lens and the camera, what's the magnification? OK, when the lens is focussed on infinity, it's 50 mm from the film, so now it's 86 mm away (v = 86). From the equation, 1/u + 1/86 = 1/50, so (calculator) u = 119. Think about the straight green lines through the centre of the lens, and it's obvious that the sizes of the object and image are proportional to their distances from the lens. So in this case, the object is a bit further away (119 mm) than the image (86 mm), and the magnification is just 86/119 = 72%.

Yes, but this is OK for simple lenses in the school physics lab. A real camera lens isn't thin, and it costs lots of money: surely the same rules don't apply?

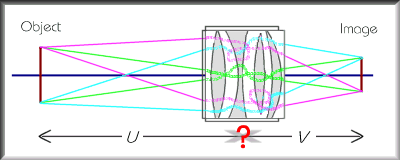Real lenses are more complicated Well, money rarely buys exemption from the laws of nature. But yes, the lens is a big thick complicated lump of glass, and what happens inside really is a bit mysterious. However, our basic equation gives the best approximation to start from, and you probably can't calculate anything more accurate unless you're in the optics lab of a large camera manufacturer.

What about sticking two lenses together?

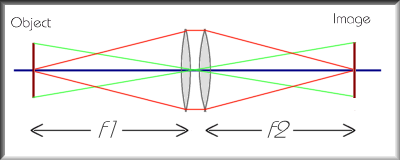Combining two focal lengths Suppose the lenses have focal lengths f1 and f2; put the two lenses together, and as a special case, put the object at the focal length f1 from the first lens. This tells us (apply the equation to the first lens) that the rays from a particular point on the object will form an image at infinity. That is, the converging power of the first lens will just make the rays parallel, as shown by the red rays between the lenses. But now, since the rays are going into the second lens parallel, by a similar argument they form the image at just the focal length f2 from the second lens. So if we just check that the combination of two lenses also acts as a lens does, which we'll do in a moment, we know that the constant quantity for the combination is 1/f1 + 1/f2. If we call the focal length of the combined lens F, this gives us another formula:

1/f1 + 1/f2 = 1/F

But we don't need to memorise this separately: we just remember that all lens calculations amount to adding reciprocals.

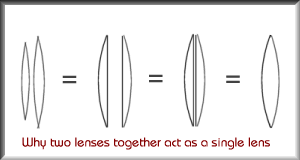
Joining two lenses to make one

Do the two lenses really make a combination lens?

Check 1: Generally from childhood experience we know that two magnifying glasses, one on top of the other, make a more powerful magnifying glass, but we can also know that a lens can easily be made with one surface face curved and the other flat. We can see that two such lenses must function together as a simple lens, simply by putting them with the flat surfaces together.

Check 2: Modern camera lenses consist of many lenses joined together, and they cost a lot of money, so it must be right, mustn't it?

Note that I've referred to the tulip as the "object", which is the optics convention. In photography it's more usually known as the "subject."

And what's a dioptre? (or a "diopter"? *)

Though you often see a close-up lens referred to as a "dioptre" - usage akin to calling an electric heater a "watt" - a dioptre is actually a unit for measuring the converging power of a lens. It's simply the reciprocal of the focal length in metres, and since everything in lens arithmetic works on reciprocals, this means that the powers of two lenses can simply be added together. The following calculator finds the effective focal length of a combination of two lenses. If you put some values in, it should be obvious how the dioptre values work.

* Dioptre or diopter? I grew up with "dioptre", but this is one of these cases where the division between British and American spelling isn't clear cut. The Shorter Oxford English Dictionary (1933) lists only the "diopter" spelling, but even that only in a different sense. For the "converging power" unit it gives "dioptric". Hmm.